-
Cet Implexe complexe me laisse perplexe

En généalogie, on dit qu'il y a implexe quand, dans un arbre généalogique "théorique" comportant 2 parents, 4 grands-parents, 8 arrière-grands-parents, etc., un ancêtre apparaît plusieurs fois.
Implexe peut être adjectif (des cases d'un arbre généalogique sont implexes) ou nom (au sens de "doublons"). Implexe désigne aussi parfois ce que nous appelons ci-dessous le taux d'implexe.
Le nombre théorique d'ancêtres d'une personne est multiplié par 2 à chaque fois que l'on remonte d'une génération. En comptant en moyenne 25 ans par génération, une personne née en 1975 a 8 ancêtres nés en 1900 (2x2x2), 128 nés en 1800, 2 048 nés en 1700, ..., 2 147 483 648 nés en 1200 alors que la population mondiale n'a atteint un milliard qu'au XIXe siècle. La différence entre le nombre théorique et le nombre réel d'ancêtres s'explique par le fait que des "doublons" (des implexes) apparaissent toujours dans l'arbre d'ascendance de tout un chacun, et ce d'autant plus vite s'il y a des mariages entre personnes apparentées à un degré proche. Ce type d'union consanguine est accentué en partie par les phénomènes d'endogamie qui poussaient (et poussent toujours) les membres de la société à trouver un conjoint au sein de la même communauté géographique, sociale, parentale, professionnelle, confessionnelle...
On peut calculer le taux d'implexe pour la génération n par la formule suivante :
taux d'implexe = (nombre d'ancêtres théorique à la génération n - nombre réel) / nombre théorique
(multiplier par 100 pour mettre en %)
Ainsi, le taux d'implexe pour la n ème génération est, en pourcentage, la part des 2^n (2 puissance n) cellules théoriques d'un arbre généalogique où les ancêtres sont comptés plusieurs fois. Pour le dire plus simplement: le taux d'implexe est le taux de "doublons".
Un taux élevé indique un grand nombre de mariages entre ancêtres apparentés. Plus l'on remonte dans les générations, plus ce taux augmente. Par exemple, les enfants d'un mariage entre cousins germains ont un taux d'implexe d'au moins 25 % pour les générations d'avant les grands-parents, car ces enfants n'ont que 6 arrière-grands-parents sur les 8 "théoriques", ce qui fait un taux de doublons au moins égal à (8-6)/8 = 0.25 = 25 %.
Le cas le plus célèbre d'implexe élevé est celui du roi d’Espagne Alphonse XIII qui, à la 11e génération, n'avait que 111 ancêtres différents au lieu des 1 024 théoriques ce qui donne un implexe de (1024 – 111) / 1024 = 89 %. (Source Wikipédia)Pour simplifier, quand deux ou plusieurs enfants d'un couple sosa sont aussi vos sosa (vous devriez n'en avoir qu'un seul par génération), on dit qu'il y a implexe.
C'est le cas pour mes sosas: 1139, 2283 et 4600 qui sont tous les trois des enfants de mon sosa 2278
 Michel LE BOURDAIS (sosa 2278) et
Michel LE BOURDAIS (sosa 2278) et  Anne MOUSSAY (sosa 2279) sont les Parents de:
Anne MOUSSAY (sosa 2279) sont les Parents de: Françoise LE BOURDAIS sosa 1139, née le le 15 novembre 1663 à Niort-la-Fontaine (53)
Françoise LE BOURDAIS sosa 1139, née le le 15 novembre 1663 à Niort-la-Fontaine (53)- Jean LE BOURDAIS
 Pierre LE BOURDAIS sosa 4600, né le 22 avril 1667 à Niort-la-Fontaine (53)
Pierre LE BOURDAIS sosa 4600, né le 22 avril 1667 à Niort-la-Fontaine (53)- Marguerite LE BOURDAIS, née le 8 avril 1668 à Niort-la-Fontaine (53)
- Jeanne, née le 4 octobre 1670 à Niort-la-Fontaine (53)
- François, né le 24 avril 1673 à Niort-la-Fontaine (53)
 Marie LE BOURDAIS sosa 2283, née le 29 juin 1681 à Niort-la-Fontaine (53)
Marie LE BOURDAIS sosa 2283, née le 29 juin 1681 à Niort-la-Fontaine (53)
Du coup je me pose la question, un individu peut-il avoir un n° sosa supérieur à celui de ses Parents ?
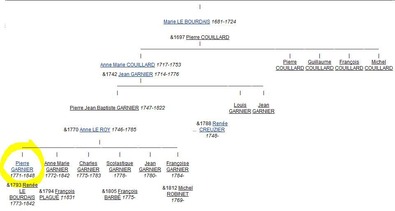
Ma sosa 2283 est de fait, la fille de mon sosa 2278Il s'avère que Marie LE BOURDAIS (sosa 2283) épouse Pierre COUILLARD (sosa 2282) le 26 novembre 1697 à Chantrigné (53), que de cette union naitra, entre autre, Anne Marie COUILLARD (sosa 1141), le 24 mars 1717 à Chantrigné. Celle-ci épousera Jean GARNIER (sosa 1140) le 27 novembre 1742 à Chantrigné.
De cette union naitra Pierre Jean Baptiste GARNIER (sosa 570) le 21 juin 1747 à Chantrigné. Pierre Jean Baptiste épousera Anne LE ROY (sosa 571) le 17 mai 1770 à Chantrigné.
Le 8 février 1771 ils donneront naissance à Chantrigné, à Pierre Garnier (sosa 574). Ce dernier épousera Renée LE BOURDAIS (sosa 575) qui s'avère être également l'Arrière Petite Fille de Pierre LE BOURDAIS (sosa 4600).
Je suis convaincu que vous avez tout compris...
 « Lawrence d'Arabie, les Héros meurent toujours deux foisDans la Série des Prénoms rares, voici Hardouine »
« Lawrence d'Arabie, les Héros meurent toujours deux foisDans la Série des Prénoms rares, voici Hardouine »